需求
了解二叉树
解决
是什么
从根节点开始,小的向左边放,大的向右边放,一层一层放下去。满足左小右大原则。
- 没有子节点的是叶子
- 子节点的个数是度
- 从根到当前节点的为一路径上节点总数是深度
- 从当前节点到最远叶子路径上的节点总数是高度
用处
用于大数据量时的反复的搜索和插入。
- 有序链表: 查找成本大 O(N), 插入成本小 O(1)
- 有序数组: 查找成本小 O(1), 插入成本大 O(N)
- 排序二叉树: 比较折中,查找时类似于二分查找 O(logN), 插入成本也小 O(logN).
打印
层序遍历
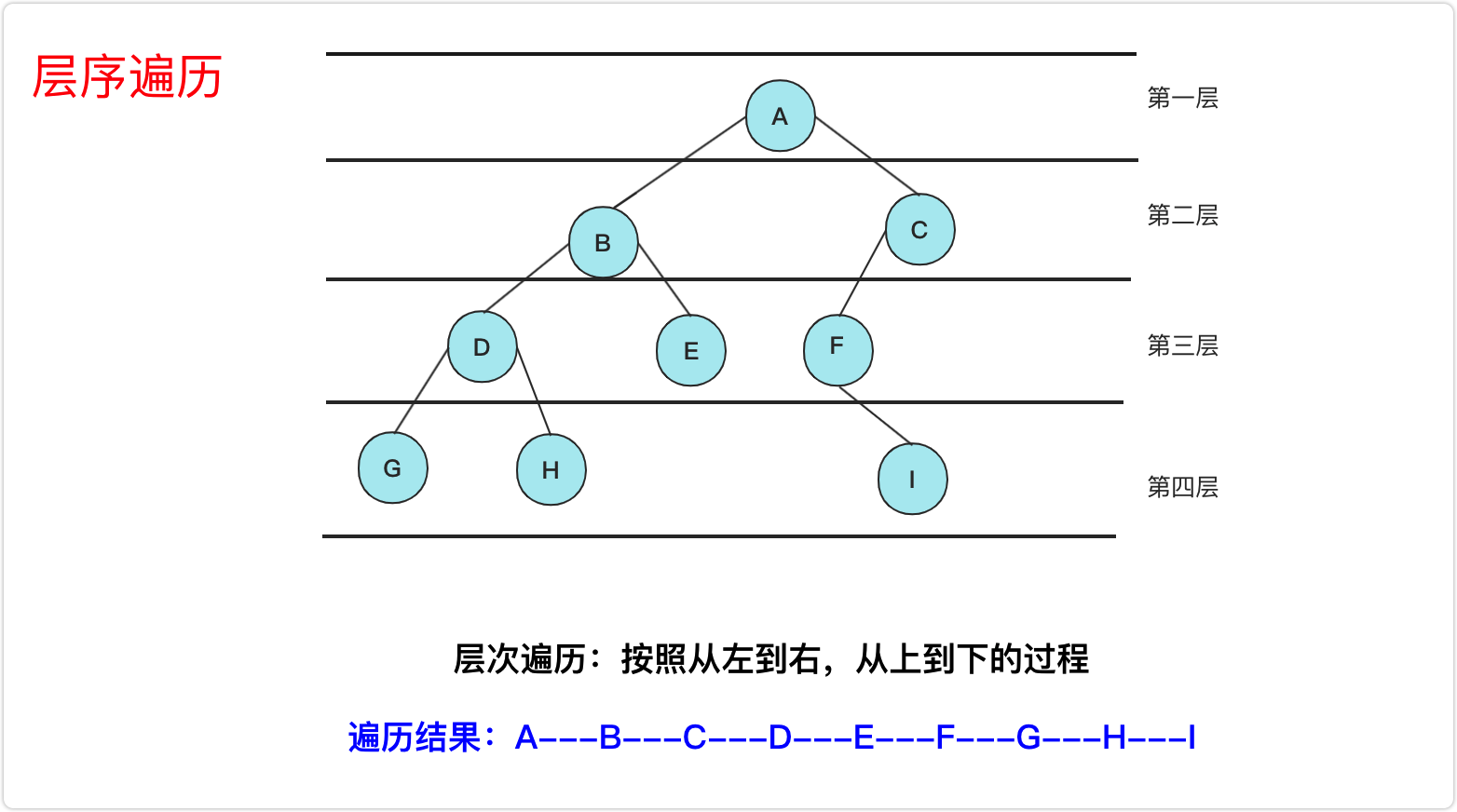
public int[] levelOrder(TreeNode root) {
int arr[]=new int[10000];
int index=0;
Queue<TreeNode>queue=new ArrayDeque<>();
if(root!=null)
queue.add(root);
while (!queue.isEmpty()){
TreeNode node=queue.poll();
arr[index++]= node.val;
if(node.left!=null)
queue.add(node.left);
if(node.right!=null)
queue.add(node.right);
}
return Arrays.copyOf(arr,index);
}
分层存储
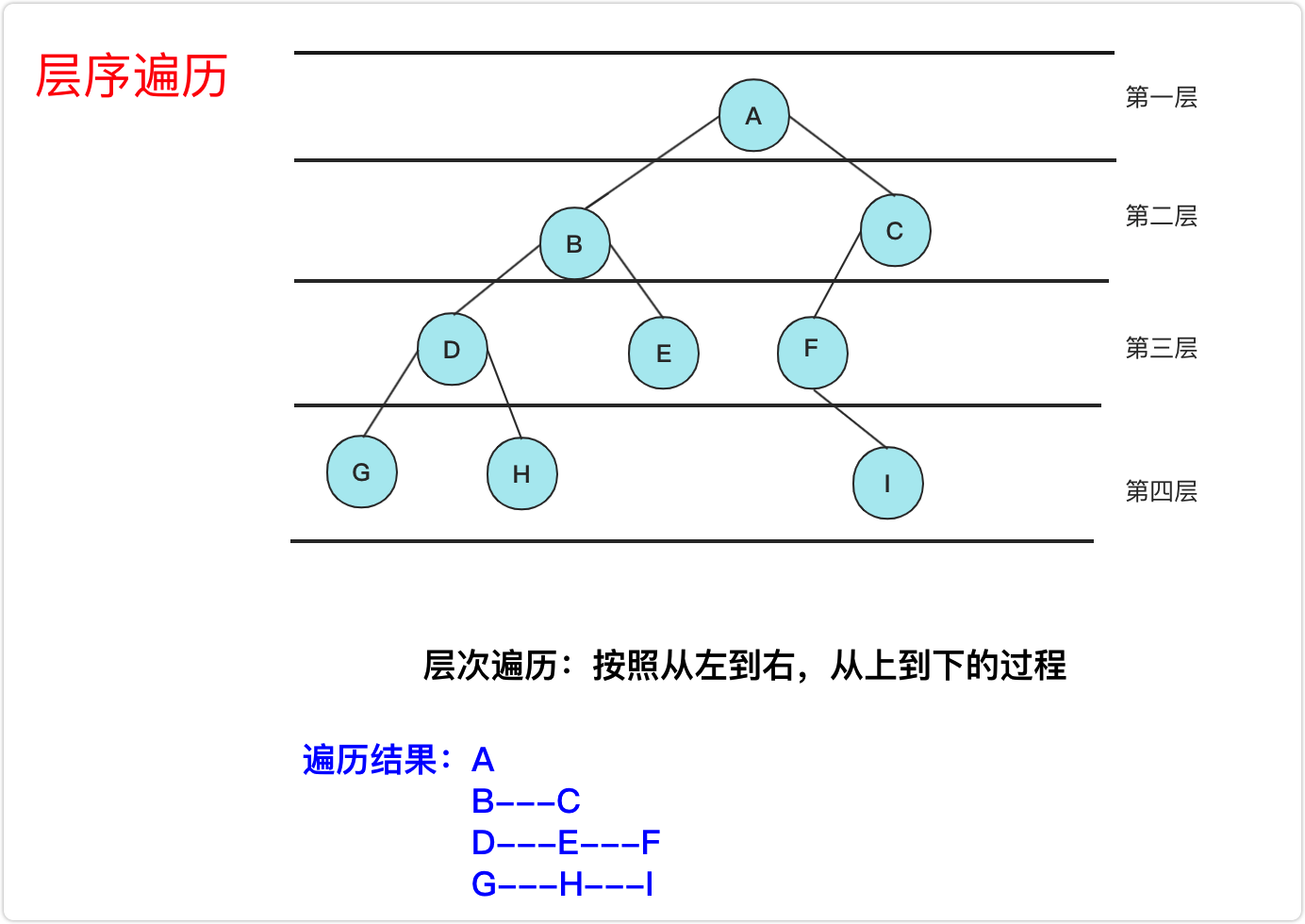
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>>list=new ArrayList<List<Integer>>();
if(root==null)return list;
Queue<TreeNode>q1=new ArrayDeque<TreeNode>();
q1.add(root);
while (!q1.isEmpty()) {
int size=q1.size();
List<Integer>value=new ArrayList<Integer>();
for(int i=0;i<size;i++)
{
TreeNode pNode=q1.poll();
if(pNode.left!=null)
q1.add(pNode.left);
if(pNode.right!=null)
q1.add(pNode.right);
value.add(pNode.val);
}
list.add(value);
}
return list;
}
之字形打印
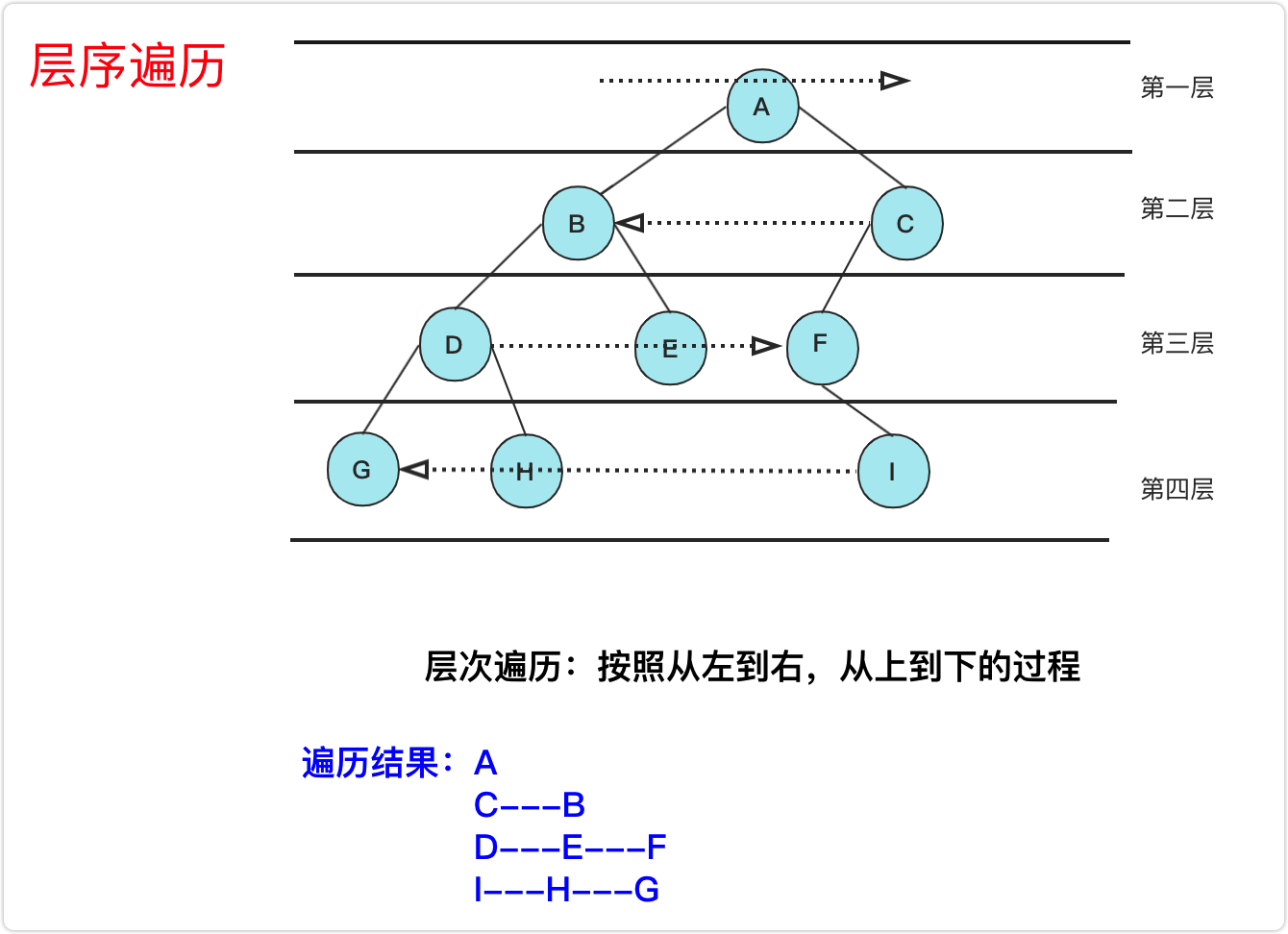
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> value=new ArrayList<>();//存储到的最终结果
if(root==null)
return value;
int index=0;//判断
Queue<TreeNode>queue=new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()){
List<Integer>va=new ArrayList<>();//临时 用于存储到value中
int len=queue.size();//当前层的数量
for(int i=0;i<len;i++){
TreeNode node=queue.poll();
if(index%2==0)
va.add(node.val);
else
va.add(0,node.val);
if(node.left!=null)
queue.add(node.left);
if(node.right!=null)
queue.add(node.right);
}
value.add(va);
index++;
}
return value;
}
遍历
前序遍历
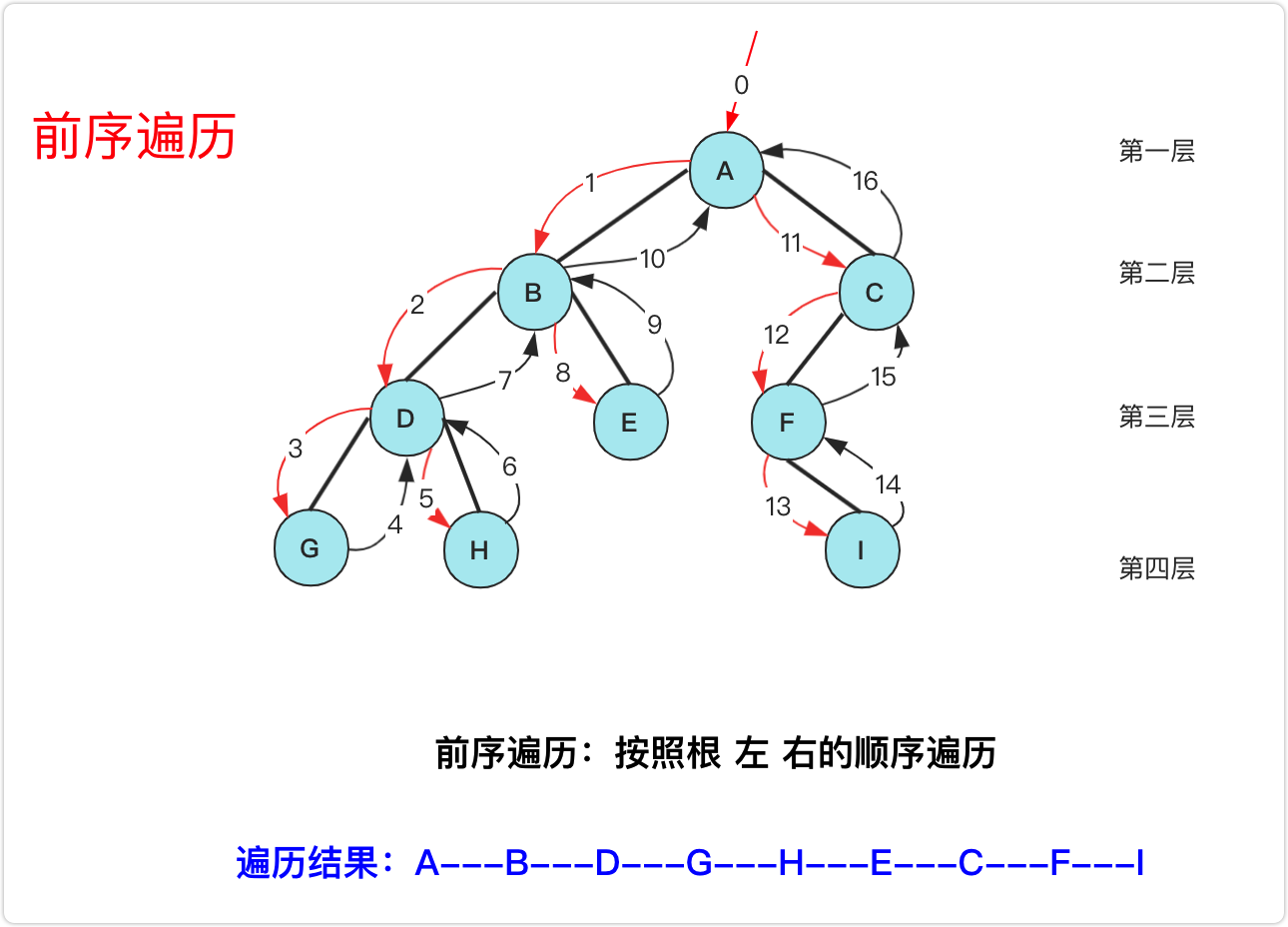
-
递归
class Solution { List<Integer>value=new ArrayList(); public List<Integer> preorderTraversal(TreeNode root) { qianxu(root); return value; } private void qianxu(TreeNode node) { if(node==null) return; value.add(node.val); qianxu(node.left); qianxu(node.right); } }
-
非递归
class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer>value=new ArrayList(); Stack<TreeNode> q1 = new Stack(); while(!q1.isEmpty()||root!=null) { while (root!=null) { value.add(root.val); q1.push(root); root=root.left; } root=q1.pop();//抛出 root=root.right;//准备访问其右节点 } return value; } }
中序遍历
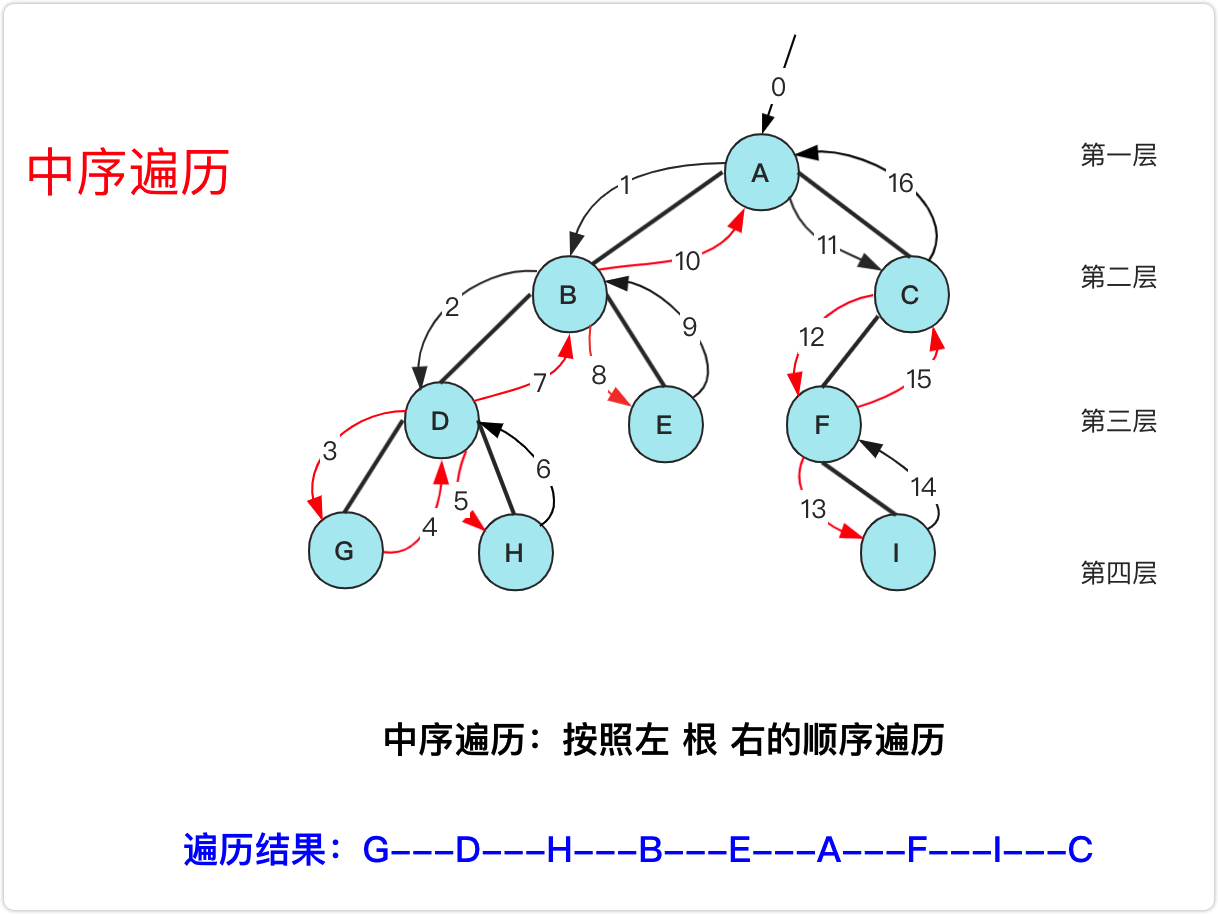
-
递归
class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer>value=new ArrayList<Integer>(); zhongxu(root,value); return value; } private void zhongxu(TreeNode root, List<Integer> value) { if(root==null) return; zhongxu(root.left, value); value.add(root.val); zhongxu(root.right, value); } }
-
非递归
class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer>value=new ArrayList<Integer>(); Stack<TreeNode> q1 = new Stack(); while(!q1.isEmpty()||root!=null) { while (root!=null) { q1.push(root); root=root.left; } root=q1.pop();//抛出 value.add(root.val); root=root.right;//准备访问其右节点 } return value; } }
后序遍历
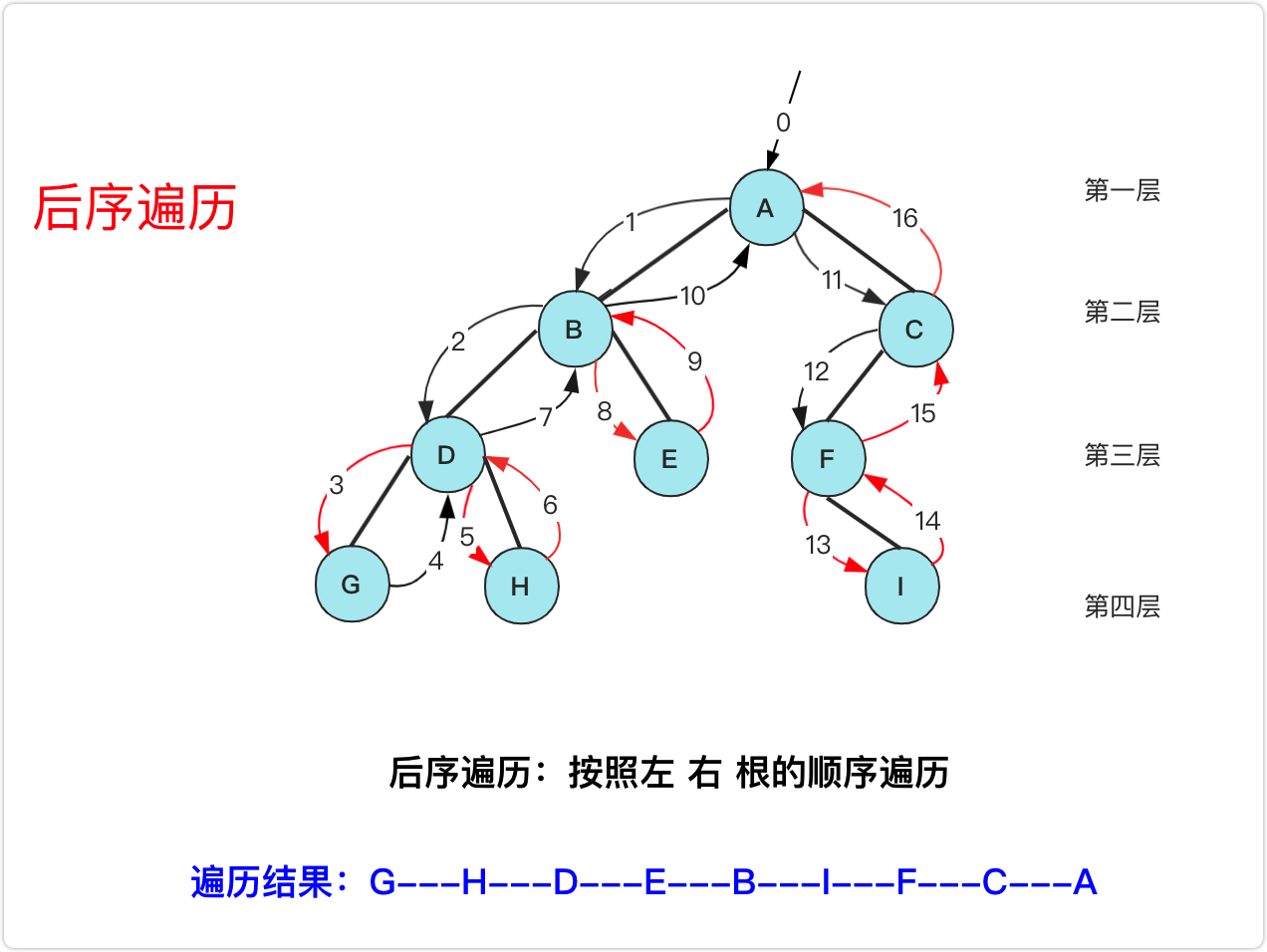
-
递归
class Solution { List<Integer>value=new ArrayList<>(); public List<Integer> postorderTraversal(TreeNode root) { houxu(root); return value; } private void houxu(TreeNode root) { if(root==null) return; houxu(root.left); houxu(root.right);//右子树回来 value.add(root.val); } }
-
非递归
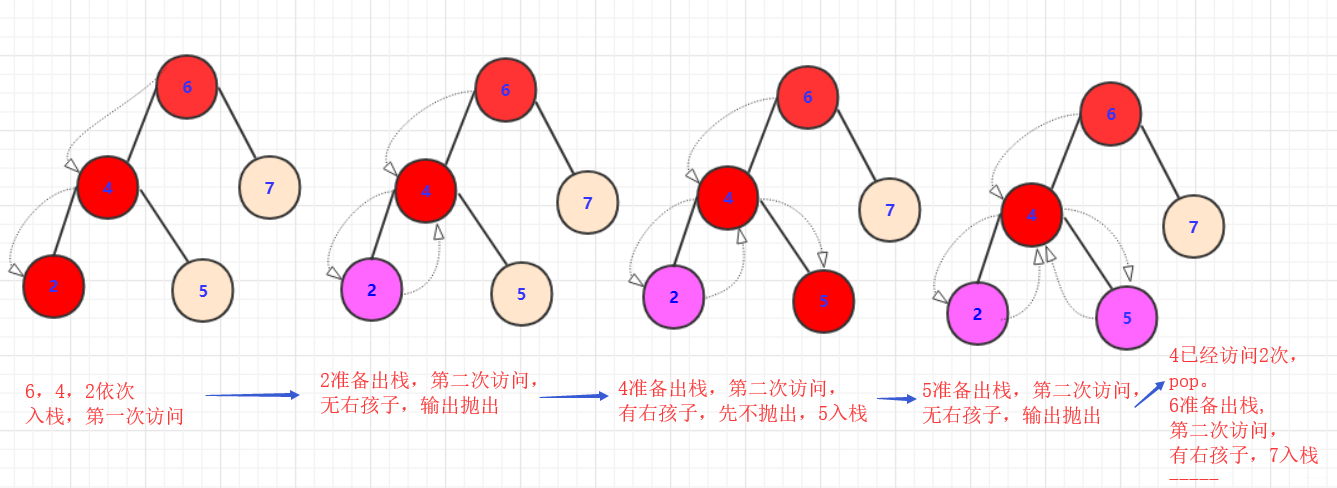
class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> value=new ArrayList(); Stack<TreeNode> q1 = new Stack(); Map<TreeNode,Integer >map=new HashMap<>(); while(!q1.isEmpty()||root!=null) { if (root!=null) { q1.push(root); map.put(root, 1); //t.value标记这个值节点出现的次数 root=root.left; } else { root=q1.peek(); if(map.get(root)==2) {//第二次访问,抛出 q1.pop(); value.add(root.val); root=null;//需要往上走 } else { map.put(root, 2); root=root.right; } } } return value; } }
-
非递归,防止 hash 冲突
class Solution { public List<Integer> postorderTraversal(TreeNode root) { TreeNode temp=root;//枚举的临时节点 List<Integer>value=new ArrayList<>(); TreeNode pre=null;//前置节点 Stack<TreeNode>stack=new Stack<>(); while (!stack.isEmpty()||temp!=null){ while(temp!=null){ stack.push(temp); temp=temp.left; } temp=stack.pop(); if(temp.right==pre||temp.right==null)//需要弹出 { value.add(temp.val); pre=temp; temp=null;//需要重新从栈中抛出 }else{ stack.push(temp); temp=temp.right; } } return value; } }
-
后序左右中,反向就是中右左,即反向前序
class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer>value=new ArrayList(); Stack<TreeNode> q1 = new Stack(); while(!q1.isEmpty()||root!=null) { while (root!=null) { value.add(root.val); q1.push(root); root=root.right; } root=q1.pop();//抛出 root=root.left;//准备访问其右节点 } Collections.reverse(value);//将结果翻转 return value; } }
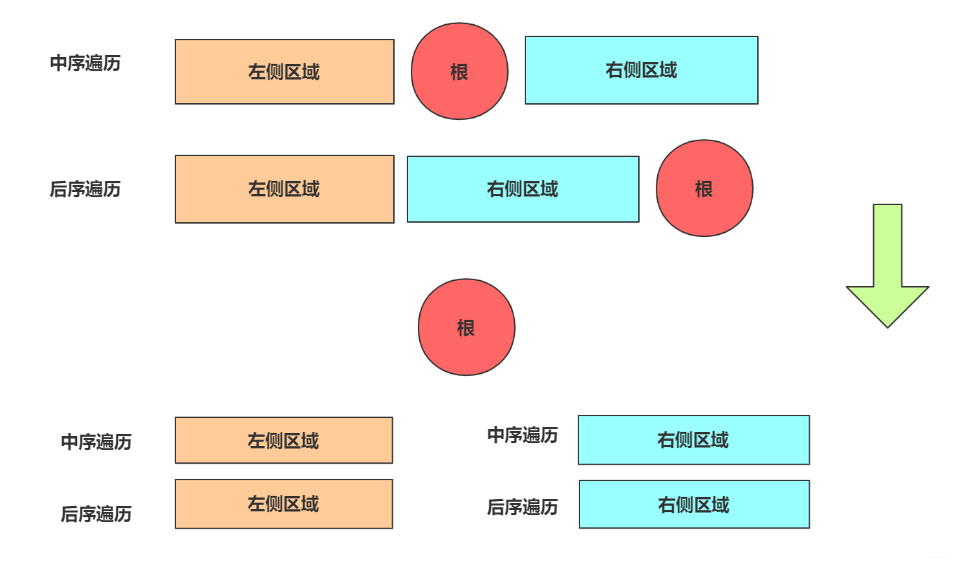
两个序列构造二叉树
前序和中序
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer>value=new ArrayList();
Stack<TreeNode> q1 = new Stack();
while(!q1.isEmpty()||root!=null)
{
while (root!=null) {
value.add(root.val);
q1.push(root);
root=root.right;
}
root=q1.pop();//抛出
root=root.left;//准备访问其右节点
}
Collections.reverse(value);//将结果翻转
return value;
}
}
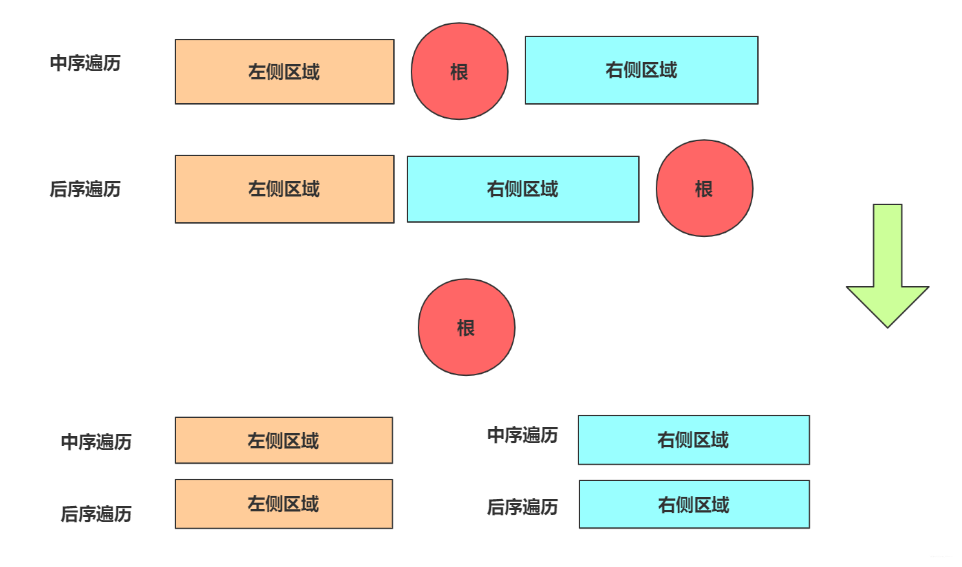
中序和后序
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode buildTree(int[] inorder,int[] postorder) {
if(postorder.length==0)
return null;
Map<Integer, Integer>map=new HashMap<Integer, Integer>();
for(int i=0;i<inorder.length;i++)
{
map.put(inorder[i], i);
}
return buildTree(postorder,0,postorder.length-1, map,0,inorder.length-1);
}
private TreeNode buildTree(int[] postorder, int postStart, int postEnd, Map<Integer, Integer> map, int inStart, int inEnd) {
// TODO Auto-generated method stub
if(postEnd<postStart||inEnd<inStart)
return null;
TreeNode node=new TreeNode(postorder[postEnd]);
int i=map.get(postorder[postEnd]);
int leftlen=i-inStart;
node.left=buildTree(postorder, postStart,postStart+leftlen-1, map, inStart, i-1);
node.right=buildTree(postorder, postStart+leftlen,postEnd-1, map, i+1, inEnd);
return node;
}
}